Worth the wait: Children trade off delay and reward in self- and other-benefiting decisions
Funding information
This research was funded by a National Science Foundation CAREER Grant (#1253676) and a National Science Foundation Graduate Research Fellowship (# DGE-1144152).
Abstract
Human prosocial behaviors are supported by early-emerging psychological processes that detect and fulfill the needs of others. However, little is known about the mechanisms that enable children to deliver benefits to others at costs to the self, which requires weighing other-regarding and self-serving preferences. We used an intertemporal choice paradigm to systematically study and compare these behaviors in 5-year-old children. Our results show that other-benefiting and self-benefiting behavior share a common decision-making process that integrates delay and reward. Specifically, we found that children sought to minimize delay and maximize reward, and traded off delays against rewards, regardless of whether these rewards were for the children themselves or another child. However, we found that children were more willing to invest their time to benefit themselves than someone else. Together, these findings show that from childhood, other- and self-serving decisions are supported by a general mechanism that flexibly integrates information about the magnitude of rewards, and the opportunity costs of pursuing them. A video abstract of this article can be viewed at: https://youtu.be/r8S0DGe7f8Q
RESEARCH HIGHLIGHTS
- Prosocial behavior fundamentally involves trading off costs to the self against rewards to the other.
- Using a modified intertemporal choice task, we found that children chose to maximize reward (stickers), minimize opportunity cost (delay), and traded off between the two.
- Children invested more time towards earning stickers for themselves, versus for another child.
- Children's tradeoffs in both other- and self-benefiting decisions followed a hyperbolic discounting function, qualitatively similar to those observed in human adults and non-human animals.
1 INTRODUCTION
Humans care about the welfare of others: We punish those who treat us or third parties poorly, make fair allocations of resources and expect others to do the same, and donate our money, time, and energy to help others with no expectation that the favor will be returned in kind. When engaging in these behaviors, we face the task of representing and comparing others’ welfare against our own (Axelrod & Hamilton, 1981; Buckholtz, 2015; Crockett, Kurth-Nelson, Siegel, Dayan, & Dolan, 2014; Delton & Robertson, 2016). Here, we focus on helping—costly behaviors that deliver benefits to others—and investigate its origins in childhood. In deciding whether and how to help others, we have to consider the effort required to help, whether this effort is worth the reward, and whether the recipient of these rewards needs and deserves our generosity. What are the origins of these capacities? Do we begin as rational altruists, trading off our costs against others’ rewards, or do we learn to do so gradually, over years of interacting with and learning from others?
The motivational and cognitive resources supporting cooperation emerge early in development. Children help others complete their goals (Eisenberg, Spinrad, & Morris, 2013; Hepach, Vaish, Grossmann, & Tomasello, 2016; Tomasello & Vaish, 2013; Vaish, Carpenter, & Tomasello, 2009; Warneken, 2016), understand social norms like fairness (Fehr, Bernhard, & Rockenbach, 2008; Kanngiesser & Warneken, 2012; McAuliffe, Blake, Steinbeis, & Warneken, 2017; Sloane, Baillargeon, & Premack, 2012) and are willing to pay a personal cost in order to help and share (McAuliffe et al., 2017; Warneken, Hare, Melis, Hanus, & Tomasello, 2007). This vast literature demonstrates that our impulse to cooperate is at the core of our social development. What representations and computations support these abilities?
Here, we build on proposals that children's prosocial behavior is best thought of as a decision-making process (Bridgers, Jara-Ettinger, & Gweon, 2016; Sommerville et al., 2018): one which integrates information about the cost of actions, the rewards they generate, and the social value of the other. Previous research provides evidence that the building blocks of reward- and cost-sensitive decision-making emerge early in development: Infants and young children tend to pursue the shortest path to a goal (Paulus & Sodian, 2015), search a location that has more rewards (Feigenson, Carey, & Hauser, 2002), plan reaches in accord with how much physical effort their actions will require (Upshaw & Sommerville, 2015), are more willing to help when less physical effort is required (Sommerville et al., 2018), and are more likely to teach other people things that are high in reward and difficult to learn (Bridgers et al., 2016). Children are also sensitive to temporal delay as a cost (Kidd, Palmeri, & Aslin, 2013; Mischel, Shoda, & Rodriguez, 1989), suggesting that they consider not only physical effort, but also opportunity cost (the loss of time available to pursue other rewards), in their action planning. Furthermore, children's own ability to delay rewards has been shown to predict their tendencies to engage in costly sharing (Garon, Johnson, & Steeves, 2011; Thompson, Barresi, & Moore, 1997), suggesting that children's own action planning is related to their prosocial behavior. Lastly, children adjust their cooperative strategies based on who benefits from their actions (Dunfield & Kuhlmeier, 2010; Engelmann, Over, Herrmann, & Tomasello, 2013; Moore, 2009), suggesting that they also take social value into account when deciding whom to benefit.
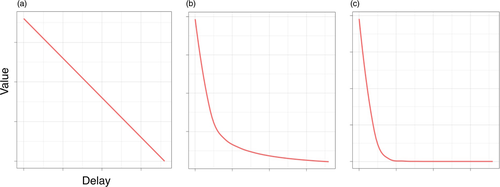
The above research, conducted in children across different age groups and using different tasks, shows that as soon as children are able to plan actions in the world, they plan over variables like cost and reward to cooperate with and help others. Here, we present a case study within this framework, and ask how and whether children trade off between delay and reward. Studies of human adults reveal tradeoffs between these factors in both prosocial and self-serving decisions: People adjust the value of monetary rewards based on its temporal delay in self-serving decisions (Berns, Laibson, & Loewenstein, 2007; Laibson, 1997) and trade off rewards delivered to another person against how socially distant that other person is (Delton & Robertson, 2016; Jones & Rachlin, 2006). What function (Figure 1) expresses children's discounting strategies, both when they work to benefit themselves and others?
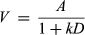 (1)
(1) (2)
(2)In the above equations, V refers to subjective value, A to reward, D to delay, and k to an individual's discounting factor. Specifically, k describes how steeply a person trades off reward against delay: Individuals who are less patient are thought to measure higher on this parameter. The key distinction between hyperbolic and exponential discounting is that exponential discounting assumes time-consistent preferences: Under exponential discounting, the difference in subjective value of a reward between now versus next week is the same as the difference in value between 52 and 53 weeks from now, whereas under hyperbolic discounting, the former difference is greater than the latter. Many past studies ask which of these functions best describes the mechanisms of temporal discounting, and the general consensus is that hyperbolic discounting provides a better fit to people's decisions (Berns et al., 2007; Green, Fristoe, & Myerson, 1994; Laibson, 1997)
1.1 Present research
In summary, previous research suggests that children are adept action planners and precocious cooperators, but no research to date provides a systematic analysis of the mechanisms underlying self- and other-benefiting choices in young children. To investigate these questions, we chose to study children at an age where they demonstrate some patience under delay (Kidd et al., 2013; Mischel et al., 1989) and robust prosocial behavior (for a review, see Warneken, 2016). We developed a series of tasks that aimed to assess whether children (1) choose to minimize delay and maximize reward and (2) trade off between these two variables in both self-serving and prosocial decisions. Based on the evidence reviewed above, we predicted that children would be rational deciders—minimizing delay, maximizing reward, and trading off delay against reward, regardless of whether their actions benefited themselves or someone else. Furthermore, we predicted that children would invest more time towards their own rewards. Lastly, our study design allows us to make inferences about the functions (Equations 1-2) that describe children's discounting behaviors.
2 METHODS
2.1 Participants
N = 32 five-year-old children (M = 5.56 years, range = 5.03–5.98, 16 girls) were recruited and included in our final sample. Sample size was determined through a simulation power analysis on the effect of delay on discounting decisions from a pilot experiment (alpha = 0.05, two-tailed, desired power = 0.8). Four additional children were tested, excluded, and replaced due to experimenter error. Recruitment and experimental procedures were approved by the Committee on the Use of Human Subjects at Harvard University.
2.2 Materials
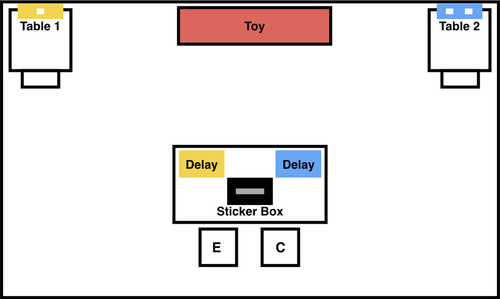
Figure 2 illustrates the setup of the experiment: one central table, where decisions were made; two payoff tables, where children waited for rewards; and a toy, which incentivized children to view delay as an opportunity cost. One payoff table was consistently associated with lower delays and rewards, and the tables were marked with blue and yellow signs to help children remember which was which. On every trial, cards displaying the delays associated with each decision were placed on each corner of the decision table, and sticker rewards were placed at the payoff tables. Children deposited all rewards earned during the game into a box at the central table. Cards with 0 to 18 squares indicated the delays of each option, where each square represented a 5-second delay. A stopwatch was used by the experimenter to keep track of delays. Children rated various aspects of the game (e.g. stickers, waiting) on a 7-point Likert scale (Figure S2). To encourage children to view the delays of the game as costly (a methodological challenge we encountered during piloting), we introduced two toys that children could play with after they completed (1) Delay and Reward decisions, and (2) Discounting decisions.
2.3 Design
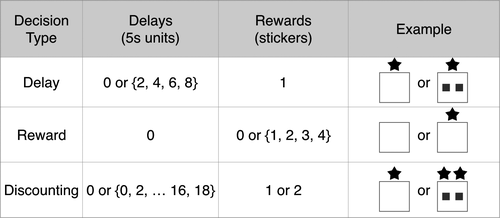
We randomly assigned children to earn sticker rewards for themselves (self condition) or for another child participant (other condition). The experiment featured three kinds of decisions (Figure 3): Delay decisions, which hold reward constant, Reward decisions, which hold delay constant, and Discounting decisions, which vary delay across a constant ratio of rewards. Children engaged in four Delay decisions, where they chose to earn 1 sticker after no delay or after {2, 4, 6, 8} 5-second units of delay, four Reward decisions, where they chose to earn 0 or {1, 2, 3, 4} stickers with no delay, and 10 Discounting decisions, where they chose to earn 1 sticker after no delay or 2 stickers after {0, 2, 4 … 18} 5-second units of delay. These delays, although far shorter than those from experiments testing decisions in human adults, allowed us to test children across many trials, using real, experienced delays rather than hypothetical ones.
We counterbalanced whether the Reward or Delay decisions came first, which table was designated as the higher reward and delay location (left or right, blue or yellow), which table was introduced first during decisions (left or right), the order of comprehension check questions and Likert scale questions, and the first anchor presented (−3 or +3) during Likert ratings across participants.
2.4 Procedure
First, the experimenter introduced an opportunity cost toy, an exciting ball machine, and asked children to rate the toy on the Likert-scale by asking, ‘How do you feel about the red zigzag machine? Do you really like or really don't like it or somewhere in between? Can you point to a face and show me?’ This toy was replaced with an equally exciting second machine before Discounting decisions. Before each decision, children were reminded that they had to choose one of the options presented before eventually gaining access to the toy. Children rated the toys very highly (M1 = 2.77, SD1 = 0.67; M2 = 2.75, SD2 = 0.57).
Next, children received an endowment of stickers in a paper bag. Children learned that these stickers were earned for them by a previous participant, and were told that in the current game, they would earn additional stickers for themselves (self condition) or for another child ‘just like you, who also likes stickers’, coming at some other time to play the game (other condition). Children did not see how many stickers were in their endowment until after the experiment.
Then, children were introduced to the study setup, where they could choose to wait some length of time, for some number of stickers, for either themselves or another child. To convey different amounts of delay to children, the experimenter showed the child a card corresponding to each option, where one square on the card referred to a 5-second delay. For instance, children saw a card with four blue squares on a particular trial and learned that ‘at the blue table, you'll have to wait 4 times [20 seconds] before you can take the stickers from the blue table and put them into the box…’. To familiarize children to the full range of delays in the experiment, children were also asked to wait the minimum and maximum delay (0 and 90 seconds, respectively).
On every decision, children chose to sit at one of the two payoff tables in order to earn the stickers at that table. The experimenter timed the delay using a stopwatch and told children that waiting is a ‘quiet part of the game’. If children spoke during delays, the experimenter reminded them of the rules. After completing the delay, children deposited the stickers from that trial in a box, and returned to the central table. If children chose an option with no delay, the stickers were available as soon as they sat down. A secondary experimenter then replaced the stickers and cards for the next trial, and the experiment continued.
Children made four Delay decisions (holding reward constant) and four Reward decisions (holding delay constant). Children then rated the delays and rewards in the game and answered comprehension questions about the setup of the Discounting decisions: (1) which table always has more and which table always has less stickers (probing their reward discrimination), (2) which table always requires more and which table requires less waiting (probing their delay discrimination), and (3) who the stickers were for: themselves or the next participant. In the other condition, we also asked (4) whether the next participant was real or pretend. The experimenter provided corrective feedback to all questions. Children then made 10 Discounting decisions: choices between earning 1 sticker now, or 2 stickers after a delay.
At the end of the experiment, children were asked to explain their decision-making strategy (‘How did you decide which table to choose in this game?’). Responses were coded for mention of the delay (e.g. ‘I didn't like waiting’) and rewards (e.g. ‘I wanted to get more stickers’). Ambiguous responses (e.g. ‘This one has more and this one has less’) were coded conservatively as mentioning neither delay nor reward. At the end of the session, children in the other condition passed on all of their earned stickers to the next participant, and children in the self condition were asked to donate 6 stickers to the next participant. These endowments were then passed forward within conditions to ensure that all subsequent participants started out with some reward, regardless of assignment to condition.
2.5 Data coding and analysis
All responses were coded online, except for children's explanations, which were transcribed and coded offline from video. All decisions including minor experimenter error (one Delay decision, two Reward decisions, and one Likert rating of a toy) were conservatively excluded from the analyses. To assess the reliability of all measures, videos from decisions and explanations in 25% of the sessions were randomly selected, cut to remove all information about assignment to condition, and re-coded by an additional researcher who was naïve to the hypotheses of the experiment. The coders agreed on 100% of responses. Data and analysis scripts can be accessed via the Open Science Framework at https://osf.io/k5twy/.
We used the lme4 package (Bates, Mächler, Bolker, & Walker, 2015) in R (Team, 2015) to implement all linear mixed effects models and generalized linear mixed effects models. We fit three classes of models: (1) null models, including intercepts only, (2) hypothesis-driven models, including additional theory-driven predictors like reward and delay, and (3) exploratory models that include additional non-theoretically driven predictors like gender. All models with repeated measures included a random intercept for participant identity. All reported p-values are two-tailed, and all t tests use Satterthwaite approximation to degrees of freedom. Bracketed values indicate 95% confidence intervals. In cases where models were nested, we used likelihood ratio tests (LRTs) to assess model fit. In all other cases, we assessed fit using the Akaike Information Criterion (AIC). We used the ggplot2 package (Wickham, 2009) to produce Figures 4 and S3–S5.
3 RESULTS
3.1 Comprehension checks
All participants correctly answered all comprehension questions regarding the Discounting decision setup. All except two participants (94%) correctly identified the recipient of the rewards. All children randomly assigned to earn stickers for the next participant affirmed that the recipient was real, not pretend.
3.2 Delay and Reward decisions
We found that during Reward decisions, wherein children chose between more and less rewards at equal delay, children chose to maximize rewards, [2.157, 8.872], B = 3.602, SE = 1.214, p = 0.003, OR = 36.672, and were equally likely to do so for themselves (93.55% of decisions) than for another child (90.63%), [−2.348, 3.408], B = 0.488, SE = 1.074, p = 0.650, OR = 1.629. We also found that during Delay decisions, wherein children chose between equal rewards at more or less delay, children chose to minimize delay, [1.165, 2.817], B = 1.384, SE = 0.281 p < 0.001, OR = 3.989, and were marginally less likely to choose the smaller delay when earning rewards for themselves (71.43%), versus another child (85.94%), [−1.955, 0.008], B = −0.906, SE = 0.469, p = 0.054, OR = 0.404. Children were no more likely to make reward-maximizing decisions as payoffs increased, [−0.312, 1.088], B = 0.333, SE = 0.340, ß = 0.374, p = 0.328, OR = 1.395. Similarly, children's tendencies to minimize delay did not vary across increases in delay, [−0.123, 0.271], B = 0.071, SE = 0.099, p = 0.474, OR = 1.074. See Figure S1.
3.3 Discounting decisions
Children chose to maximize rewards and minimize delays independently, but did they trade off between these two variables? A set of hypothesis-driven models were fit to assess whether children's decisions (1) were affected by the recipient manipulation, (2) changed over length of delay, and (3) followed a hyperbolic function.
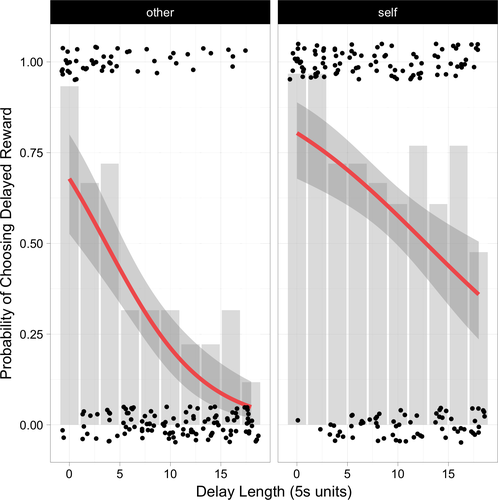
A hypothesis-driven model adding the predictors of untransformed delay length (0, 2, 4….18 5-second units) and recipient (self versus other) revealed that children were less likely to choose the higher delayed reward as its delay increased, [−0.286, −0.157], B = −0.218, SE = 0.033, ß = −1.253, p < 0.001, OR = 0.804, and more tolerant of delays when earning rewards for themselves, [0.800, 3.673], B = 2.136, SE = 0.699, p = 0.002, OR = 8.466. This model provided a better fit than the null model, X2(2) = 71.513, p < 0.001. An additional model fitting an interactive effect between recipient and delay indicated that children's responses to changes in delay did not differ across conditions, [−0.024, 0.222], B = 0.097, SE = 0.062, ß = 0.557, p = 0.121, OR = 3.808. See Figure 4 for decisions across children and Figure S5 for individual decisions.
An explicit comparison of children's discounting parameter, k (Kirby, 2000), across conditions revealed that children discounted less steeply in the self condition (M = 0.035, SD = 0.026) than in the other condition (M = 0.058, SD = 0.034), [−0.045, −0.001], B = −0.023, SE = 0.011, ß = −0.726, t(30) = −2.172, p = 0.038. In sum, children made traded off delay against reward during both self- and other-benefiting decisions, but were generally less tolerant of delays when earning stickers for another child versus themselves.
What mathematical function best describes children's discounting behavior? To ask whether children's sensitivity to delay during discounting is best expressed as a linear, hyperbolic, or exponential function of delay length, we compared three models using the Akaike Information Criterion (AIC): the above model including untransformed linear delay, D, a second model including a hyperbolic function on delay (Equation 1), 1/1+D, and a third model including an exponential function (Equation 2) on delay, e−D.1 A comparison of model AICs revealed that the hyperbolic model (313.19) provided better fit for decisions than both the linear (323.84) and the exponential (438.04) models. An exploratory model including subjective value under hyperbolic discounting and 2 additional predictors, age in months and sex, revealed that girls were more patient than boys, [0.534, 3.207], B = 1.776, SE = 0.646, p = 0.006, OR = 5.906, and no effect of age, [−0.111, 0.244], B = 0.065, SE = 0.085, ß = 0.243, p = 0.449 OR = 1.067. This model provided a better fit than the simpler hyperbolic model by a likelihood ratio test, X2(2) = 7.986, p = 0.018.
In summary, we found that (1) children were less willing to invest time towards stickers for others versus themselves (2) both kinds of decisions involved tradeoffs between delays and rewards, and (3) a hyperbolic function best captured these decisions.
3.4 Exploring the predictors of children's discounting strategies
What other variables predict children's discounting behavior? We tested whether children's valuation of the delays and rewards in the experiment (measured by their Likert ratings of stickers and waiting) and their reported strategies (measured by verbal explanations of their decision-making process) explain variance in their discounting behavior. However, these measures were generally not predictive of children's discounting decisions above and beyond the subjective value of the rewards and who these rewards were for. The only positive finding from this analysis revealed that children who reported thinking about the stickers during their decisions (e.g. ‘Because the blue table has more stickers than the yellow table’, ‘Because I just wanted more stickers’) were more likely to choose the higher, delayed reward, [0.277, 3.353], B = 1.728, SE = 0.741, p = 0.020, OR = 5.628. For full results from this model, see Table 1. See Supplemental Material available online for additional analyses of children's subjective ratings and reported strategies.
| Fixed effect | B | SE | z | p | 95% CI | OR |
|---|---|---|---|---|---|---|
| Intercept | 1.383 | 0.658 | 2.101 | 0.036* | 0.110, 2.844 | 3.988 |
| Recipient | 1.593 | 0.651 | 2.444 | 0.015* | 0.342, 3.039 | 4.916 |
| Subjective value | 1.640 | 0.296 | 5.542 | <0.001*** | 1.131, 2.304 | 5.156 |
| Sex | 1.704 | 0.617 | 2.759 | 0.006** | 0.517, 3.071 | 5.493 |
| Age in months | −0.141 | 0.319 | −0.443 | 0.657 | −0.811, 0.516 | 0.868 |
| Mentioned delays | −0.808 | 0.591 | −1.366 | 0.172 | −2.066, 0.392 | 0.446 |
| Mentioned rewards | 1.728 | 0.741 | 2.330 | 0.020* | 0.277, 3.353 | 5.628 |
| Delay Likert rating | 0.151 | 0.375 | 0.403 | 0.687 | −0.635, 0.925 | 1.163 |
| Reward Likert rating | 0.026 | 0.324 | 0.081 | 0.936 | −0.621, 0.719 | 1.026 |
- *p < 0.05; **p < 0.01; ***p < 0.001, all two-tailed
- Model AIC = 309.4; BIC = 347.1; log-likelihood = −144.7; deviance = 289.4
- Number of participants: 32, σ2=1.408
4 DISCUSSION
Human cooperation is supported by early-emerging motivations to deliver benefits to others at costs to the self. We used an intertemporal choice task to investigate the cognitive mechanisms that support these tradeoffs in childhood. We found that children sought to minimize delay, maximize reward, and traded off between delay and reward during both self- and other-benefiting decisions. We also found that children were less willing to invest time if someone else's stickers were at stake, suggesting that they trade off reward against delay more steeply for prosocial than self-serving decisions. Lastly, we found that like human adults (Berns et al., 2007) and non-human animals (Kacelnik & Marsh, 2002; Mazur & Biondi, 2009; Rosati et al., 2007), children's discounting strategies were captured by a hyperbolic function on the delay of this reward that expresses its subjective value. These results build on past work showing that our abilities to plan and cooperate emerge in early childhood, and contribute a mechanistic proposal for how costs and rewards are integrated into children's self- and other-benefiting decisions.
This research raises questions about the fundamental mechanisms of prosocial behavior. First, our results do not reveal whether children shifted their valuation of reward, delay, or both, when making self- versus other-benefiting choices. Although we did not observe a relationship between children's Likert ratings of reward and delay and their discounting behavior, it is possible that other measures of value may help to clarify the computations that supported children's decisions. We also do not claim that hyperbolic discounting provides a complete description of or explanation for children's decisions. Our findings suggest that hyperbolic discounting provides a better fit to the data relative to other functions, and future studies can enrich our understanding of the quantitative tradeoffs underlying children's decision-making.
Next, our case study does not address the question of how children discount reward by social value (how much they value other people's utilities relative to our own). Research in human adults suggests that we discount others’ rewards by their social value (Albrecht, Volz, Sutter, Laibson, & von Cramon, 2011; Delton & Robertson, 2016; Jones & Rachlin, 2006; Strombach et al., 2015), and developmental work can further investigate how children integrate social and temporal distance in their prosocial decisions.
More generally, this work supports the possibility that from an early age, patience is not only a growing resource (Atance & Jackson, 2009; Green, Fry, & Myerson, 1994; Harbaugh, Krause, & Berry, 2001) but also one that is strategically deployed based on context (Kidd et al., 2013). Further studies of the flexibility of intertemporal choice, and decision-making more broadly, can reveal how we come to represent time as a precious resource and delay as a cost. While we suggest that children's representation of value over time follows a hyperbolic function, our study leaves open whether other kinds of cost, like physical or mental effort, would trade off against reward in the same way.
Finally, these results leave open the origins and development of this mechanism. Are the decision-making processes recruited by infants and toddlers in previous studies of prosocial behavior the same ones used by children in this task? How do culture and circumstance shape these mechanisms? Studies charting this task space across different populations and across childhood can clarify the development of the competencies that these tasks are meant to measure. Overall, these results demonstrate that by early childhood, children recruit a rich decision-making process for self-serving and prosocial action that integrates many sources of information. Children appear to engage in rational altruism, a process supported by early-emerging motivations to benefit others at a cost to the self, and tradeoffs between how much good they can generate and at what cost.
ACKNOWLEDGEMENTS
This research was funded by a National Science Foundation CAREER Grant (#1253676) to FW and a National Science Foundation Graduate Research Fellowship (#DGE-1144152) to SL. The authors thank Alexandra Rosati for helpful discussion, and Daniel Kim, Courtney Liang, Katey Usatii, Eroica Rene, Oorja Batra, Randi Vogt, and Natalie Benjamin for research assistance.
AUTHOR NOTE
All authors wrote the paper and designed the research, SL and GG collected the data. SL analyzed the data.