About why there is a shift from cardinal to ordinal processing in the association with arithmetic between first and second grade
Abstract
Digit comparison is strongly related to individual differences in children's arithmetic ability. Why this is the case, however, remains unclear to date. Therefore, we investigated the relative contribution of three possible cognitive mechanisms in first and second graders’ digit comparison performance: digit identification, digit–number word matching and digit ordering ability. Furthermore, we examined whether these components could account for the well-established relation between digit comparison performance and arithmetic. As expected, all candidate predictors were related to digit comparison in both age groups. Moreover, in first graders, digit ordering and in second graders both digit identification and digit ordering explained unique variance in digit comparison performance. However, when entering these unique predictors of digit comparison into a mediation model with digit comparison as predictor and arithmetic as outcome, we observed that whereas in second graders digit ordering was a full mediator, in first graders this was not the case. For them, the reverse was true and digit comparison fully mediated the relation between digit ordering and arithmetic. These results suggest that between first and second grade, there is a shift in the predictive value for arithmetic from cardinal processing and procedural knowledge to ordinal processing and retrieving declarative knowledge from memory; a process which is possibly due to a change in arithmetic strategies at that age. A video abstract of this article can be viewed at: https://youtu.be/dDB0IGi2Hf8
RESEARCH HIGHLIGHTS
- We investigated which cognitive processes underlie the well-established relation between digit comparison performance and arithmetic ability in first and second graders.
- In both age groups, digit ordering ability explained unique variance in digit comparison performance.
- As previously observed in adults, digit ordering fully mediated the relation between digit comparison and arithmetic in second graders.
- In first graders, the reverse was true and digit comparison fully mediated the relation between digit ordering and arithmetic.
- This suggests a shift from cardinal to ordinal information and from procedural to declarative knowledge, possibly due to a shift in arithmetic strategies.
1 INTRODUCTION
In the domain of numerical cognition, digit comparison performance (i.e., the ability to indicate which of two presented digits is numerically larger) has been used for decades as a central tool to index individual differences in both children's and adults’ number processing skills. In particular, the performance on this task has been supposed to index knowledge about the cardinality of the number symbol (i.e., the fact that the Arabic symbol “5″ refers to five items; Goffin & Ansari, 2016; Lyons & Beilock, 2013). In addition, numerous studies have consistently shown that individual differences in the performance on this digit comparison task are a robust predictor of individual differences in arithmetic ability (e.g., Budgen & Ansari, 2011; Castronovo & Göbel, 2012; De Smedt, Verschaffel, & Ghesquière, 2009; Göbel, Watson, Lervåg, & Hulme, 2014; Holloway & Ansari, 2009; Kolkman, Kroesbergen, & Leseman, 2013; Landerl & Kölle, 2009; Lyons, Price, Vaessen, Blomert, & Ansari, 2014; Moyer & Landauer, 1967; Mussolin, Meijas, & Noël, 2010; Sasanguie, De Smedt, Defever, & Reynvoet, 2012; Sasanguie, Göbel, Moll, Smets, & Reynvoet, 2013; Vanbinst, Ghesquière, & De Smedt, 2012; Vogel, Remark, & Ansari, 2015; Xenidou-Dervou, Molenaar, Ansari, van der Schoot, & van Lieshout, 2016; for a review, see De Smedt, Noël, Gilmore, & Ansari, 2013; for a meta-analysis, see Schneider et al., 2017). Moreover, studies investigating participants with mathematical learning difficulties have observed that they perform worse on a digit comparison task compared to control participants (Ashkenazi, Mark-Zigdon, & Henik, 2009; Brankaer, Ghesquière, & De Smedt, 2014; De Smedt & Gilmore, 2011; Landerl, Bevan, & Butterworth, 2004; Landerl, Fussenegger, Moll, & Willburger, 2009; Rousselle & Noël, 2007; Vanbinst, Ghesquière, & De Smedt, 2014; for a meta-analysis, see Schwenk et al., 2017).
Despite the crucial role that digit comparison performance plays in explaining individual differences in arithmetic, to date little is known about why this is the case. For the first time and only very recently, Sasanguie, Lyons, De Smedt, and Reynvoet (2017) investigated in adults which cognitive processes play a role when performing a digit comparison task and, more crucially, whether these processes could account for (a part of) the well-established relationship between digit comparison performance and arithmetic ability. They reasoned that in order to perform a digit comparison task, several cognitive skills are necessary. First, one has to visually identify the presented symbol as a digit. This digit identification process has been shown to be related to arithmetic ability in children (e.g., Cirino, 2011; Cui et al., 2017; Koponen, Salmi, Eklund, & Aro, 2013; Mazzocco & Grimm, 2013; Purpura, Baroody, & Lonigan, 2013; van der Sluis, de Jong, & van der Leij, 2004; Vanbinst, Ghesquière, & De Smedt, 2012, 2015) and adults (Sasanguie et al., 2017). Second, children might need to link the visually presented digit to its phonological counterpart, namely the verbal number word. This phonological–orthographic mapping process which children learn during development (although there is still no consensus about when and in which order this exactly occurs; Benoit, Lehalle, Molina, Tijus, & Jouen, 2013; Purpura & Ganley, 2014) has also been shown to be associated to arithmetic ability in both children (Lyons et al., 2014) and adults (Sasanguie & Reynvoet, 2014). Third, to perform a digit comparison task, one additionally has to understand the ordinal relations among digits in a sequence; for example, that 5 comes after 4 and before 6 (Sury & Rubinsten, 2012; Turconi, Campbell, & Seron, 2006). Again, in the past few years, it has been observed that this digit ordering ability—that is, the ability to judge whether symbolic numbers are in numerical order—is positively related to the score on an arithmetic test for both children (Lyons & Ansari, 2015; Lyons et al., 2014) and adults (Goffin & Ansari, 2016; Lyons & Beilock, 2013; Morsanyi, O'Mahony, & McCormack, 2017; Vos, Sasanguie, Gevers, & Reynvoet, 2017).
Sasanguie et al. (2017) observed that digit identification and especially digit ordering ability were predictors of adults’ performance on a digit comparison task. In addition, path analyses revealed that the relation between digit comparison and arithmetic was fully mediated by digit ordering, whereas the reverse was not true (i.e., digit comparison did not mediate the relation between digit ordering and arithmetic). Therefore, these results suggested that performance on the digit comparison task does not purely reflect cardinality, but also contains a distinct ordinal component and that it is this latter component which is responsible for the association with arithmetic ability in adults.
Previous developmental studies have demonstrated that the relation between digit comparison performance and arithmetic ability changes over time. For example, Lyons et al. (2014) investigated the predictability of eight numerical skills for arithmetic during the time course of primary school. Results revealed that symbolic number processing skills explained most of the variance in children's arithmetic ability in all grades, but that the essence of this relation changed during development. Whereas at the beginning of elementary school, digit comparison performance was most predictive for arithmetic, its predictive capacity decreased with age. In contrast, digit ordering ability was not predictive for arithmetic in the first grade but its predictability increased steadily from second grade onwards. Therefore, these results suggest that the relative importance of symbolic number processing for arithmetic shifts from cardinal to ordinal processing over development.
Consequently, in the current study, we investigated whether the same cognitive processes underlie digit comparison in children as is the case in adults and, even more importantly, whether (some of) these processes can account for the observed developmental change in the relationship between digit comparison performance and arithmetic. We examined this in first and second graders, because Lyons et al. (2014) observed that the predictors of arithmetic are changing at this point in development. In the current study, in addition to an arithmetic test and a digit comparison task, children performed three tasks assessing the three candidate predictors of digit comparison performance: fast identification, audiovisual digit–number word matching and digit order judgement. First, we examined which of the three candidate predictors explained unique variance in the digit comparison task. Second, we investigated whether the predictors that did explain unique variance could explain the relation between digit comparison and arithmetic. In line with Sasanguie et al. (2017) and taking into account the developmental shift reported by Lyons et al. (2014), we hypothesised that digit ordering ability would become more important for arithmetic from second grade onwards only. Consequently, we predicted that only for this age group digit ordering ability would account for some or all of the variance in the relation between digit comparison and arithmetic. In contrast, we hypothesised that digit comparison would remain the best (and only) predictor of arithmetic ability for the first graders.
2 METHOD
2.1 Participants
Two hundred and sixty-four children from different elementary schools in Flanders participated. From the first graders (n = 122), three participants were excluded from the analyses because of missing data (i.e., illness and technical problems). Another 17 participants were discarded because they performed below chance level (50%) on one of the experimental tasks. Finally, 10 participants were removed from the analyses because they were too slow or made too many errors in one of the experimental tasks (i.e., 3 SD above or below the group mean). The final sample consequently consisted of 92 first graders (43 males, Mage = 6.28 years; SD = 0.45). From the second graders (n = 141), nine participants were discarded from the analyses because of missing data, 10 participants were excluded because they performed below chance and 12 participants were removed from the analyses because they were too slow or made too many errors in one of the experimental tasks (i.e., 3 SD above or below the group mean). On the basis of these criteria the final sample consisted of 110 second graders (43 males, Mage = 6.93 years, SD = 0.32).1 Informed consent forms were obtained from all children's legal guardians.
2.2 Procedure1
First, participants performed the four experimental tasks (i.e., fast identification, audiovisual digit–number word matching, digit order judgement and digit comparison) in groups of five accompanied by an experimenter. The order in which the tasks were presented was counterbalanced using a Latin square design (Gravetter & Forzano, 2006). A short break was provided between each task. In addition, participants performed a paper-and-pencil arithmetic test, which was administered by classroom testing (i.e., the instructions were read aloud for the whole group and then the participants were requested to fill in their own page).
All experimental tasks (see Figure 1) were conducted using a 15-inch colour screen connected to a computer running the Windows 7 operating system. The experiment was presented by E-prime Professional software, version 2.0 (Psychological Software Tools, Pittsburgh, PA, USA). In all of the tasks, a trial started with a fixation cross for 600 ms. Subsequently, two stimuli were presented (one on the left and one on the right side of the screen) which remained on the screen for 1000 ms. Afterwards, a blank screen appeared until a response was detected. Participants could respond during the stimulus presentation or during the blank screen. After the participants responded, an intertrial interval of 1500 ms followed. Participants were instructed to respond by pressing “a” to indicate the left stimulus or “p” to indicate the right stimulus on an AZERTY keyboard. The visual stimuli were displayed in white against a black background (Courier New Font 40, Bold). The same applied to the audiovisual digit–number word matching task, except that in this task, an auditorily presented stimulus and two visual stimuli were presented simultaneously. The auditory stimulus (i.e., a verbal number word) was digitally recorded (sampling rate 44.1 kHz, 16-bit quantization) by a Dutch female speaker. Recordings were band-pass filtered (180–10,000 Hz), resampled at 22.05 kHz, and matched for loudness. The sounds were presented binaurally through loudspeakers at about 65 dB SPL. On all tasks, subjects were instructed to respond as quickly and as accurately as possible. Each task was preceded by five practice trials in which feedback was provided. There was no feedback during the experimental trials.
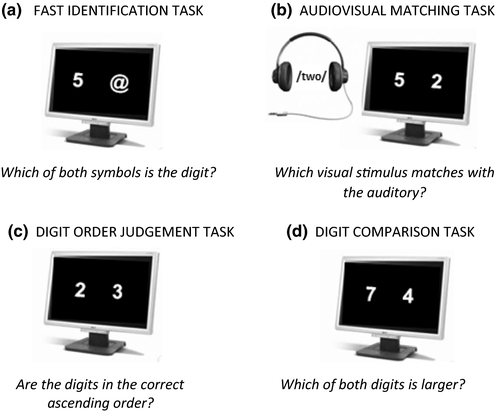
2.3 Measures
2.3.1 Experimental tasks
Fast identification task
The stimuli of the fast identification task were single digits (2–8) and randomly chosen symbols ($, #, £, @, § and €). Participants were instructed to indicate which of the two presented stimuli was the digit. The digit stimuli were presented equally on the left (n = 7) and on the right side of the screen (n = 7), resulting in 14 trial combinations. Each combination was presented five times resulting in a trial list of 70 trials.
Audiovisual digit–number word matching task
A number word was presented auditorily together with two visually presented stimuli (digits 2–8). Participants had to choose whether the right or left visually presented digit matched with the auditory number word. In half of the trials, the number word matched the left digit and in half of the trials the number word matched the right digit. Furthermore, the distance between the two visually presented digits was manipulated by distinguishing trials with a distance of one (e.g., 2–3) and trials with a distance of three (e.g., 2–5). This resulted in two conditions of 16 trials which were each presented twice, resulting in a total trial list of 64 trials.
Digit order judgement task
Two single digits (2–8) were presented on the screen and participants were instructed to indicate whether or not these stimuli were presented in left-to-right ascending order. Stimuli were counterbalanced between the left and right side of the screen (i.e., each combination of stimuli was presented in an ascending and a descending order). Furthermore, distance was manipulated by distinguishing between distance one and distance three, which resulted in two conditions of eight trials each. These eight trials were presented four times for every distance, so that the final trial list again consisted of 64 trials.
Digit comparison task
The trial list was identical to the one used in the digit order judgement task. In the digit comparison task, participants were instructed to choose which of two presented stimuli was numerically larger.
2.3.2 Standardized arithmetic test
Participants’ arithmetic ability was tested with the Tempo Test Arithmetic (De Vos, 1992). Following the test guidelines, the first and second graders only completed the first two subtests of this timed paper-and-pencil test (i.e., addition and subtraction problems). First and second graders completed the exact same test. Per subtest, 40 items of increasing complexity were presented (e.g., in the addition subtest, the first item is 1+1, and the last item is 54+27). Participants were given one minute to solve as many problems as possible. One point was awarded for each correct item, with a maximum of 80 points.
3 RESULTS
First, we examined whether first and second graders differed in their performance on the experimental tasks and the standardized arithmetic test because we hypothesised different results for both groups. Second, we examined—for each group separately—the relation between digit comparison and the candidate predictors and which of the candidate predictors could explain unique variance in the digit comparison task. Finally, using digit comparison as predictor and arithmetic as outcome variable, we entered the unique predictors of digit comparison into a mediation model to see whether the predictors could account for (some or all of) the relation between digit comparison performance and arithmetic.
3.1 Overall performance
The mean accuracies and median reaction times are presented in Table 1 (Grade 1) and Table 2 (Grade 2). Bivariate correlations between accuracies and reaction times showed that, in most of the tasks, participants responded more slowly in order to be more accurate. To account for this speed–accuracy trade-off (SAT), adjusted reaction times—also referred to as “inverse efficiency”—were derived by dividing RT scores by accuracy scores (i.e., RT/ACC). These adjusted RTs increased proportionally to the number of errors and remained unchanged when accuracy was 100% (for a similar procedure, see also Simon et al., 2008). The adjusted RTs were used in all further analyses.
| Digit identification | Audiovisual matching | Digit order judgement | Digit comparison | |
|---|---|---|---|---|
| ACC (proportion) | .95 (.04) | .89 (.09) | .75 (.14) | .81 (.13) |
| RT (msec) | 761 (279) | 995 (288) | 1291 (682) | 1082 (446) |
| Correlation ACC–RT | .20 | .31** | .06 | .27** |
- *p < .05; **p < .01.
| Digit identification | Audiovisual matching | Digit order judgement | Digit comparison | |
|---|---|---|---|---|
| ACC (proportion) | .96 (.04) | .91 (.07) | .78 (.14) | .86 (.08) |
| RT (msec) | 637 (94) | 872 (125) | 1462 (579) | 892 (238) |
| Correlation ACC–RT | .17 | .31** | .49** | .29** |
- *p < .05; **p < .01.
To check whether first and second graders indeed performed differently on the experimental tasks and the standardized test, independent samples t tests were conducted. Whenever the sphericity assumption was violated, Greenhouse-Geisser correction was applied. Second graders were significantly more accurate than first graders on all experimental tasks (i.e., t(108.84) = 4.29, p < .001 for the digit identification task; t(123.59) = 4.87, p < .001 for the digit comparison task and t(120.73) = 4.91, p < .001 for the audiovisual digit–number word matching task)—except for the digit order judgement task (t(145.90) = −.71, p = .482). Moreover and most crucially, second graders performed significantly (M = 27.48 out of 80, SD = 7.33) better than first graders (M = 22.59 out of 80, SD = 7.11) on the arithmetic test, t(200) = −4.79, p < .001.
In line with previous studies (e.g., Turconi et al., 2006; Sasanguie et al., 2017), ascending trials (e.g., 2–3) of the digit order judgement task were analysed separately to examine whether this task really addressed order processing (i.e., deciding whether stimuli are presented in the ascending order or not), and participants did not rely on for instance comparison strategies (i.e., deciding which one is larger) to solve this task. According to Turconi et al. (2006), the presence of a reversed distance effect (RDE; i.e., faster and more accurate responses when the distance between digits is smaller) in the ascending trials suggests order-specific processes such as serial scanning or direct recognition of order. In the first graders, there was no significant RDE present in the ascending trials, t(91) = −.46, p = .650, but still ascending trials with distance one were, on average, processed 188 ms faster than ascending trials with distance three. By contrast, as expected, no reversed but a significant standard distance effect (DE; i.e., faster and more accurate responses when the distance between digits is larger) was observed in the digit comparison task: ascending trials with distance three were processed 308 ms faster than ascending trials with distance one, t(91) = 2.21, p = .030.
In the second graders, a significant RDE was observed in the digit order judgement task, t(109) = −2.33, p = .022, with the ascending trials with distance one processed 191 ms faster than the ascending trials with distance three. In the digit comparison task, a standard DE was observed, with the ascending trials with distance three processed 169 ms faster than the ascending trials with distance one, t(109) = 7.66, p < .001.
3.2 First grade
3.2.1 Relations with digit comparison
First, the cognitive underpinnings of digit comparison were examined by investigating which of the three candidate predictors showed a relation with digit comparison. Table 3 displays the bivariate correlations between the experimental tasks. Significant relations were observed between all the candidate predictors and digit comparison.
| 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|
| 1 | Arithmetic | 1 | ||||
| 2 | Digit identification | −.32** | 1 | |||
| 3 | Audiovisual matching | −.36** | .69** | 1 | ||
| 4 | Digit order judgement | −.31** | .68** | .70** | 1 | |
| 5 | Digit comparison | −.51** | .47** | .47** | .61** | 1 |
- *p < .05; **p < .01.
Second, we investigated which of the candidate predictors explained unique variance in digit comparison performance. A multiple regression analysis was conducted with digit comparison as the dependent variable (Table 4). Collinearity between the tasks imposed no problem, since all variance inflation factors (VIF) were ≤ 2.35 and therefore within an acceptable range (Field, 2009). Results showed that only the digit order judgement task explained unique variance in the performance on the digit comparison task, suggesting that individuals who are more proficient at comparing two digits process the ordinal relations among digits in a sequence more rapidly.
| Independent variables | Standardized β | t | p |
|---|---|---|---|
| Digit identification | .09 | .72 | .475 |
| Audiovisual matching | .06 | .48 | .629 |
| Digit order judgement | .50 | 3.99 | <.001 |
| F(3, 88) = 17.76, p < .001, R2 = .38** | |||
- *p < .05; **p < .01.
3.2.2 Accounting for the relation between digit comparison and arithmetic
After pinpointing the cognitive underpinnings of digit comparison, we examined whether these processes could account for the relation between digit comparison and arithmetic. As only digit order judgement explained unique variance in digit comparison performance, this task was indicated as potential mediator of the relation between digit comparison and arithmetic ability. A (bootstrapped) mediation analysis was conducted using the Preacher and Hayes (2008) SPPS “MEDIATE” macro. A mediation analysis reveals whether there is a significant indirect effect (quantified as the product of the unstandardized path coefficients, ab) of the mediator(s) that explains some portion of the total effect (written as c) observed between the predictor and outcome variable. The remaining (unmediated) direct effect of the predictor on the outcome variable is indicated as c′. In this structure, the model is limited by the assumption that c = ab + c′. In deviation from a standard multiple regression analysis, this explicitly tests what portion of the relation between digit comparison and arithmetic can be explained by the mediating variable. If ab is significant but c is not, then this is inferred as full mediation; when both ab and c are significant, this is inferred as partial mediation (Preacher & Hayes, 2008). Our conclusions about statistical validity are based on the confidence intervals, and in particular whether the confidence intervals include 0.
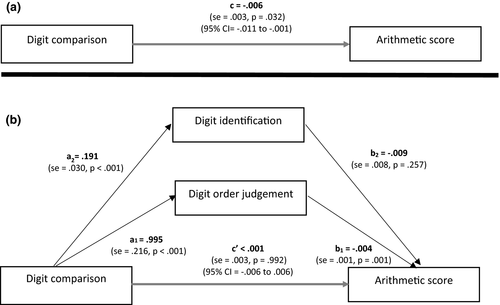
Figure 2 presents the mediation results for the first graders with arithmetic as outcome variable, digit comparison as predictor, and digit order judgement as mediator. Digit order judgement was not a significant mediator of the relation between digit comparison and arithmetic: bootstrap point estimate, ab < .001; SE = .001; 95% CI = −.002 to .002; p = .979, suggesting that although digit order judgement contributes to the variance in digit comparison performance, digit order judgement does not explain the relation between digit comparison and arithmetic.
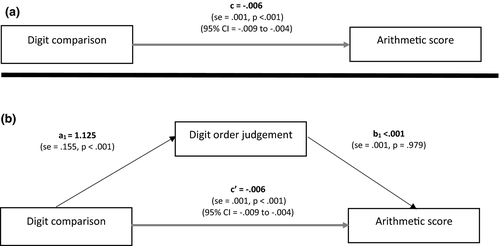
Because this study contains cross-sectional data, we also tested the opposite mediation model, that is, whether the relation between digit order judgement and arithmetic is mediated by digit comparison. Results showed a full mediation. We observed a significant total effect, path coefficient c = −.002; SE = .001; 95% CI = −.003 to −.001, p = .003, and a significant effect of the mediator variable digit comparison, ab = −.002; SE = .001; 95% CI = −.003 to −.001; p < .001. This concerned a full mediation since the direct effect of digit order judgement on arithmetic was no longer significant, path coefficient c′ < .001; SE = .001; 95% CI = −.002 to .002; p = .979, indicating that the relation between digit order judgement performance and arithmetic ability was totally accounted for by the performance on the digit comparison task. Thus, while digit order judgement did not explain the relation between digit comparison and arithmetic, digit comparison fully explained the relation between digit order judgement and arithmetic.
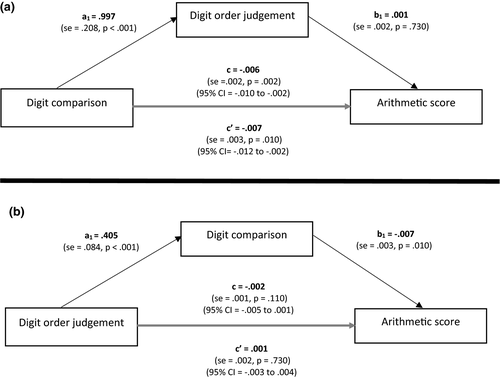
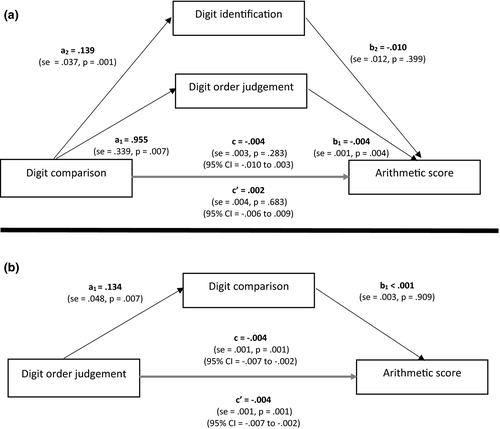
In first graders, the RDE in the digit order judgement task was not significant, although the ascending trials with a small distance were processed faster than the ascending trials with a large distance. Therefore, we examined on an individual level which strategy was applied by each child in that task and subsequently divided the children between those who showed a RDE (n = 36) and those who did not (n = 56). Mediation analyses were conducted for each group separately. In the first graders showing a RDE in the digit order judgement task, the mediation model (Figure 3) showed that digit order judgement was not a significant mediator between digit comparison and arithmetic, ab = .001; SE = .003; 95% CI = −.003 to .006; p = .734. The reversed mediation model (i.e., with digit order judgement as predictor, digit comparison as mediator, and arithmetic as outcome) showed no significant direct effect and no significant total effect of digit order judgement on arithmetic. However, there was an indirect effect of digit comparison on arithmetic, ab = −.003; SE = .001; 95% CI = −.006 to −.001; p = .020. In the first graders who did not show a RDE in the digit order judgement task, the mediation model (Figure 4) showed that digit order judgement was not a significant mediator between digit comparison and arithmetic, ab < −.001; SE = .001; 95% CI = −.003 to .002; p = .777. The reversed mediation model, however, demonstrated a total effect of digit ordering on arithmetic. Furthermore, an indirect effect of digit comparison on arithmetic was observed, ab = −.002; SE = .001; 95% CI = −.003 to −.001; p = .004. This concerned a full mediation because the total effect c was completely explained by the mediator variable digit comparison and there was no longer a significant direct effect of digit order judgement on arithmetic (i.e., the c′ path).
3.3 Second grade
3.3.1 Relations with digit comparison
With regard to second graders, we also first examined which cognitive components underpin digit comparison performance by investigating which of the three candidate predictors showed a relation with digit comparison. Table 5 displays the bivariate correlations between the experimental tasks showing significant relations between all of the candidate predictors and digit comparison.
| 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|
| 1 | Arithmetic | 1 | ||||
| 2 | Digit identification | −.22* | 1 | |||
| 3 | Audiovisual matching | −.11 | .60** | 1 | ||
| 4 | Digit order judgement | −.38** | .29** | .10 | 1 | |
| 5 | Digit comparison | −.21* | .53** | .30** | .41** | 1 |
- *p < .05; **p < .01.
Next, we investigated which of the candidate predictors explained unique variance in digit comparison performance by conducting a multiple regression analysis in which digit comparison was used as dependent variable. Collinearity between the tasks imposed no problem since all the variance inflation factors were ≤ 1.71 and therefore within an acceptable range (Field, 2009). The results displayed in Table 6 indicate that only digit identification and digit order judgement explained unique variance in the performance on the digit comparison task. These analyses suggest that the ability to compare two digits is related to (1) the ability to rapidly identify the symbol that is presented as a digit and (2) the ability to rapidly process the ordinal relations among digits in a sequence.
| Independent variables | Standardized β | t | p |
|---|---|---|---|
| Digit identification | .44 | 4.29 | <.001 |
| Audiovisual matching | .01 | .08 | .933 |
| Digit order judgement | .28 | 3.33 | .001 |
| F(3, 106) = 18.62, p < .001, R2 = .35** | |||
- *p < .05; **p < .01.
3.3.2 Accounting for the relation between digit comparison and arithmetic
We investigated whether the processes involved in digit comparison in second graders could account for the relation between digit comparison and arithmetic. Similar to what we did for first graders, we ran a (bootstrapped) mediation analysis using the Preacher and Hayes (2008) SPPS “MEDIATE” macro for simultaneously testing multiple mediators within a single analysis. Arithmetic was the outcome variable and the performance on the digit comparison task served as predictor. Both digit identification and digit order judgement (i.e., the unique predictors of digit comparison) were entered as mediators.
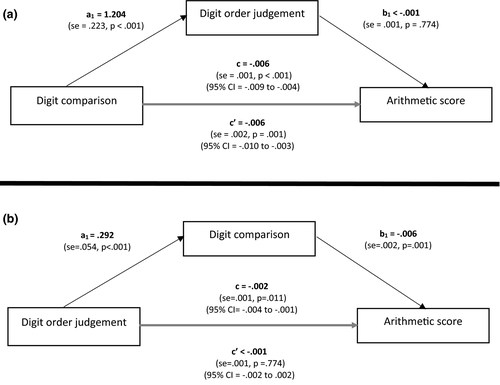
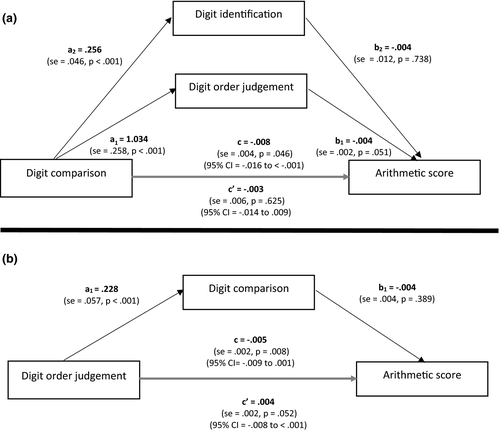
Figure 5 displays the mediation results for second graders. Only digit order judgement was a significant (full) mediator of the relation between digit comparison and arithmetic: bootstrap point estimate ab = −.004; SE = .002; 95% CI = −.008 to −.001; p = .006. Note that this was a full mediation because the total effect c was completely accounted for by the mediator variable and c′ no longer had a significant direct effect. Digit identification was not a significant mediator: bootstrap point estimate ab = −.002; SE = .002; 95% CI = −.005 to .002; p = .268. In summary, this mediation analysis indicated that knowledge about the ordinal sequence of digits, in particular, plays a crucial role in explaining the relation between digit comparison performance and arithmetic.
We also ran the opposite mediation model, that is, with digit order judgement as predictor, arithmetic as outcome and digit comparison performance as mediator variable. Results demonstrated a significant total effect, path coefficient c = −.004; SE = .001; 95% CI = −.006 to −.002, p < .001, and a significant direct effect, path coefficient c′ = −.004; SE = .001; 95% CI = −.006 to −.002; p < .001, yet no significant effect of the mediator variable digit comparison, bootstrap point estimate ab < −.001; SE < .001; 95% CI = −.001 to .001; p = .555. These results suggest that while digit order judgement fully explained the relation between digit comparison and arithmetic, digit comparison could not account for the relation between digit order judgement and arithmetic.
As we did with the first graders, in second graders we also examined on an individual level which strategy each child applied in that task and divided the children between those who showed a RDE (n = 56) and those who did not (n = 54). Mediation analyses were separately conducted for each group. For the second graders showing a RDE in the digit order judgement task, the mediation model (Figure 6) showed that digit order judgement was a significant mediator between digit comparison and arithmetic, ab = −.004; SE = .002; 95% CI = −.010 to −.001; p = .046. The reversed mediation showed a significant direct effect and total effect, but crucially no indirect effect of digit comparison on arithmetic, ab < .001; SE = .001; 95% CI = −.001 to .001; p = .913. For the second graders who did not show a RDE in the digit order judgement task, the mediation model (Figure 7) also showed that digit order judgement fully mediated the relation between digit comparison and arithmetic, ab = −.004; SE = .003; 95% CI = −.012 to < −.001; p = .080. The reversed mediation demonstrated a significant total effect, but no indirect effect of digit comparison on arithmetic, ab = −.001; SE = .001; 95% CI = −.004 to .001; p = .409.
4 GENERAL DISCUSSION
Sasanguie et al. (2017) recently identified in adults the possible cognitive underlying mechanisms when performing digit comparison, namely digit identification, digit–number word matching and digit ordering ability. Moreover, they showed that digit ordering ability fully mediated the relation between digit comparison performance and individual differences in arithmetic. Lyons et al. (2014) showed that in children, the predictability of digit comparison performance and digit ordering ability for arithmetic changed over development: Whereas in first graders cardinality (i.e., the sum of elements) is related most to arithmetic, from second grade onwards, digit ordering ability (i.e., the position of an element in a sequence) seems to become increasingly important. In the current study we therefore examined whether the same cognitive processes are predictive for digit comparison performance in first graders and second graders as is the case in adults and whether these candidate predictors can also account for some or all of the relation between digit comparison performance and arithmetic in children.
Similar to those for adults (Sasanguie et al., 2017), the results of the current study with children demonstrated that in both age groups all cognitive candidate predictors were related to digit comparison and that, of those predictors, digit ordering ability was the only or the best predictor of digit comparison performance. In order to examine whether digit ordering ability could consequently account for some or all of the relation between digit comparison and arithmetic, mediation analyses were conducted. The results of these mediation analyses differed between the age groups. As hypothesised, the performance on the digit order judgement task did not account for the relation between digit comparison and arithmetic in first graders, whereas in second graders this was the case, similar to adults. Moreover, reversed mediation models using digit order judgement as predictor, digit comparison as mediator, and arithmetic as outcome showed that whereas digit comparison fully mediated the relation between digit order judgement and arithmetic in first graders, this was no longer the case in second graders.
Next, because it is possible that there are large individual differences in how the children recruit digit ordering ability when performing the digit order judgement task (Vogel et al., 2015), separate mediation analyses were conducted for children who showed a RDE in the digit order judgement task and those who did not, and this for each grade separately. Together, these results showed that, regardless of whether children showed a RDE or not, digit ordering ability never mediated the relation between digit comparison and arithmetic in first graders (see Figures 3, 4), whereas in second graders, on the other hand, this was always the case (see Figures 6, 7). In line with what was previously demonstrated by Lyons et al. (2014), these results therefore suggest that comparison strategies (and thus cardinal information) in first graders are responsible for the observed relation between digit comparison performance and arithmetic, whereas from second grade onwards, the performance on the digit order judgement task takes over and becomes a better predictor of arithmetic, regardless of exactly which strategy the children apply when performing the digit order judgement task (and hence show a RDE or not). In order to test the latter hypothesis more directly, we conducted additional mediation analyses for those children who showed a RDE and those who did not, collapsed across grades (see Supplemental Data 1 and 2). In line with our hypothesis, for the collapsed group of first and second graders who showed a RDE (and thus process order similarly), digit ordering ability did not mediate the relation between digit comparison and arithmetic—whereas, by contrast, this was the case when the same mediation analysis was ran separately for the second graders who showed a RDE. This suggests that the observation that digit ordering ability mediates the relation between digit comparison and arithmetic in second grade but not in first grade is not due to a change in digit ordering ability.
Consequently, two questions remain unanswered at this point: (1) When children do not show a RDE in the digit order judgement task, then what exactly are they doing when performing this task? And (2) if the different mediation patterns observed in first and second graders cannot be attributed to a change in digit ordering ability, which mechanism is then responsible for this data pattern?
With regard to the first issue it must be mentioned that the group of children who did not show a RDE (either in first or second grade) showed a significant standard DE (i.e., faster and better performance on trials with a large distance compared to trials with a small distance, an effect that is typically observed when performing a digit comparison task; Moyer & Landauer, 1967). One could therefore reason that children who demonstrated a standard DE in the digit order judgement task most probably used comparison strategies in order to perform this task. For two reasons this is not very plausible, however. First, following a similar reasoning reported by Vogel et al. (2015), if the standard DE on the digit order judgement task reflects the use of comparison strategies, a correlation would be expected between the standard DE observed in the digit comparison task and the standard DE observed in the digit order judgement task, and this was neither the case for first graders (r(90) = .07, p = .514) nor for second graders (r(108) = .15, p = .116). Second, if the standard DE on the digit order judgement task observed in the second graders reflects comparison strategies, different mediation results would be expected for the second graders who showed a standard DE on the digit order judgement task and for the second graders who showed a RDE on the digit order judgement task, and this was also not the case. Indeed, regardless of whether the second graders showed a RDE or a standard DE, the performance on the digit order judgement task in both cases fully mediated the relationship between digit comparison and arithmetic. Together, these results at least suggest that both standard DEs observed in the digit comparison and the digit order judgement task, respectively, index different cognitive constructs and that the standard DE observed in the digit order judgement task most probably does not index the use of comparison strategies. It remains, however, an open question why some children, when they are not using comparison strategies, demonstrate such a standard DE when performing a digit order judgement task. In order to get full insight into the cognitive strategies that children use when performing digit ordering, further research should use verbal reports of the participants’ trial-by-trial assessment to see which strategies they used.
With regard to the second issue, the mediation analyses in Figures 3, 5-7 and in the Supplemental Data have demonstrated that it is implausible that a change in digit ordering ability is responsible for the fact that digit ordering ability mediates the relation between digit comparison and arithmetic in second graders, but not in first graders. Therefore, the crucial question remains why ordinal knowledge only becomes more predictive for arithmetic from second grade onwards, whereas (some) children already process order in a similar way in the first grade (see the observation that some first graders showed a RDE). Why does this shift in predictability from digit comparison performance/cardinality to digit ordering ability occur precisely between first and second grade?
In order to answer this question, it is important to briefly sketch the latest evidence about which mechanisms are at play when processing order. Previous recent research (Sasanguie et al., 2017; Vos et al., 2017) has suggested that to solve the digit order judgement task, participants have to activate associations between the digits themselves from their long-term memory, based on a chaining mechanism (i.e., inter-item associations are formed between adjacent items and each item serves as a trigger for the previous or the next item in the sequence; e.g., 3 triggers 4; Serra & Nairne, 2000). Furthermore, Lyons and Beilock (2013) suggested that making ordinal judgements about digits possibly relies on retrieval processes. Considering the relation between digit ordering ability and arithmetic, it has therefore been suggested that these long-term stored associations are key in explaining individual differences in arithmetic (Sasanguie et al., 2017). In other words, the better participants are at retrieving associations between digits from their long-term memory, the better their scores are on an arithmetic test. Moreover, some studies with adults have shown that there is also a relation between the order processing of non-numerical sequences and arithmetic, suggesting that the relation between order processing and arithmetic might be domain-general (Franklin, Jonides, & Smith, 2009, Morsanyi et al., 2017; Vos et al., 2017). However, it remains to be studied whether the same applies to children and whether non-numerical order processing is already related to arithmetic early on in development.
Consequently, because it is likely that these long-term stored numerical associations underlie digit ordering ability and its relation with arithmetic, the increasing predictability of digit order judgement for arithmetic is possibly due to the increasing focus of mathematics education on retrieving information from long-term memory, especially from second grade onwards. Mathematics education focuses on acquiring knowledge which can be roughly divided into three categories (Miller & Hudson, 2007), namely conceptual knowledge (i.e., acquiring concrete information and the relation between these parts of information), procedural knowledge (i.e., following a set of sequential steps to solve a particular problem), and declarative knowledge (i.e., retrieval of information from memory). When declarative knowledge comes into play, in many contexts a shift might occur from learning via conceptual and procedural to learning via declarative knowledge (Ashcraft, 1982). Also in arithmetic, first grade children initially learn to solve simple arithmetic problems by relying on procedural knowledge, that is, a set of sequential steps they have to take to solve those problems. From second grade onwards, however, children start to learn the multiplication tables, for instance, which then puts more efficient strategies at their disposal. From that moment, they can—if appropriate and possible in the context—rely on declarative knowledge, that is, information that is automatically retrieved from memory. This latter strategy can be applied in multiplication (Koshmider & Ashcraft, 1991), but also in simple addition (Ashcraft, 1982; Barouillet & Lépine, 2005), or in most general simple arithmetic problems (Busch, Schmidt, & Grube, 2015), such as those used in the arithmetic test in the current study. When turning back to the cognitive processes involved in digit comparison and in explaining its relation to arithmetic, comparison might relate to conceptual and procedural knowledge (i.e., first identifying the quantities the digits represent—i.e., their “cardinality”—and next compare them), whereas digit ordering ability might rather rely on declarative knowledge (i.e., retrieving the associations between the items from the counting list from long-term memory or the “ordinality” of the digits). In other words, the observation of a relation between digit ordering ability and arithmetic in second grade might thus be due to similar processes occurring (i.e., retrieving declarative knowledge from memory) in both the digit order judgement task and the arithmetic test. In sum, the reason why digit ordering ability only becomes increasingly important for arithmetic from second grade onwards (and is, for instance, not predictive for arithmetic in first graders in the current study) might be because there is an increasing focus on declarative knowledge in mathematics education from that time onwards. The observation that in first graders who showed a RDE, there was no direct relation between digit ordering and arithmetic could be interpreted as supportive to this reasoning: in these children, there might be no relation between digit ordering and arithmetic because comparison/procedural knowledge remains their main strategy in order to solve arithmetic problems. By contrast, in the second graders who showed an RDE, there was a relation between digit ordering and arithmetic, possibly because these children used the declarative knowledge (i.e., ordinality) at their disposal in order to solve the arithmetic test.
A direct consequence of this hypothesis that ordinality is specifically important for arithmetic when one uses the retrieval of declarative knowledge as a solution strategy, is that processing speed might play an important role: The faster one can retrieve ordinal sequences from long-term memory (i.e., declarative knowledge; see Sasanguie et al., 2017, for similar reasoning), the better one will score on an arithmetic test (which is indeed per definition a math fluency test in which speed plays a role). Therefore, it should be mentioned that, by contrast, it is less plausible that ordinal processing will be equally predictive for other types of mathematics tests, such as, for example, untimed broader/curriculum-based mathematics tests in which retrieval of declarative knowledge is only one of many strategies. Furthermore, it must be acknowledged that the hypothesis about a shift in predictive value from cardinality to ordinality for arithmetic being due to a shift from relying on procedural knowledge to relying on declarative knowledge was not explicitly tested in the current study and it requires future research to address this hypothesis in an experimental way. Besides investigating the development of which strategies are at play when performing a digit order judgement task via strategy reports (see the suggestion above), the different strategies used to solve arithmetic problems in first and second graders could also be unravelled via this method.
To conclude, the current study was the first to unravel the well-established relation between digit comparison performance and arithmetic in children who are in first and second grade. The results revealed that the performance on this digit comparison task is an important predictor of arithmetic in first and second grade, but that the cognitive mechanisms underlying this relation are dynamically changing over development. Whereas the relation between digit comparison and arithmetic is primarily driven by cardinality processing in first graders, the underlying mechanism of this relation rapidly shifts towards ordering ability (which might reflect efficient retrieval of long-term stored associations), possibly because of the larger focus on retrieval of declarative knowledge in mathematics education at that time (e.g., multiplication tables).
ACKNOWLEDGEMENTS
Delphine Sasanguie is a postdoctoral research fellow of The Research Foundation - Flanders ( www.fwo.be). This research was also supported by the Research Fund KU Leuven and the study was approved by the local ethics committee. The authors would like to thank Jasper Beyens, Lisa Fierens, Britt Geudens and Sybrentje van Ermen for their help with the data collection.